满嘴都是糖果

二叉树遍历是二叉树中最基本也是最重要的算法

二叉树遍历算法有：

前序遍历：依据中-左-右顺序对二叉树进行遍历节点
中序遍历：依据左-中-右顺序对二叉树进行遍历节点
后续遍历：依据左-右-中顺序对二叉树进行遍历节点
层序遍历：依据二叉树的深度，从上到下，在每层中依据从左到右的顺序遍历节点

二叉树结构代码

class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
}

前序遍历

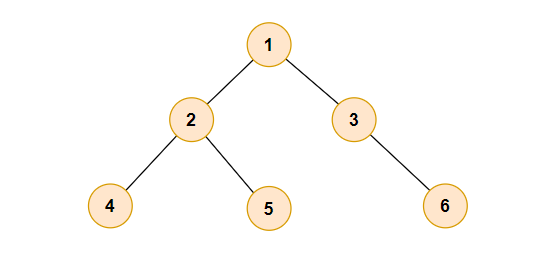
在上图二叉树中执行前序遍历算法得到的结果将会是

递归算法

public List<Integer> preorderTraversal(TreeNode root){
        List<Integer> ans = new LinkedList<>();
        preorderDfs(root, ans);
        return ans;
    }

    private void preorderDfs(TreeNode node, List<Integer> ans) {
        if (node==null)
            return;
        ans.add(node.val);
        preorderDfs(node.left,ans);
        preorderDfs(node.right,ans);
    }

迭代算法

递归算法较为简单，重点需要掌握的是迭代算法

 public List<Integer> preOrderTraversal(TreeNode root) {
        List<Integer> ans = new LinkedList<>();
        if (root == null)
            return ans;
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            if (node!=null){
                ans.add(node.val);
                stack.push(node);
                node = node.left;
            }else
            	node = stack.pop().right;
        }
        return ans;
    }

利用栈模拟递归栈来实现迭代算法，使用两层while递归。

第一层循环条件为栈不为空，或者当前需要处理的节点不为空(主要是用来弥补第一次循环中，栈为空的情况)。

第二层循环条件为当前需要处理的节点不为空，此循环内作用是一直遍历完左节点。由于是前序遍历，循环体内首先访问当前节点的数值，当前节点可以视为在当前迭代中扮演的是根节点的角色，之后将当前节点入栈，以便在遍历完左节点之后，访问右节点。那访问右节点自然就是在当前循环结束之后，通过栈获取右节点。

中序遍历

在上图中执行中序遍历算法得到的结果将会是

递归算法

public List<Integer> inorderTraversal(TreeNode root){
        List<Integer> ans = new LinkedList<>();
        inorderDfs(root, ans);
        return ans;
    }

    private void inorderDfs(TreeNode node, List<Integer> ans) {
        if (node==null)
            return;
        inorderDfs(node.left, ans);
        ans.add(node.val);
        inorderDfs(node.right,ans);
    }

迭代算法

同上，迭代法更为重要

public List<Integer> inOrderTraversal(TreeNode root) {
        List<Integer> ans = new LinkedList<>();
        if (root == null)
            return ans;
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            if (node!=null){
                stack.push(node);
                node = node.left;
            }else{
                node = stack.pop();
                ans.add(node.val);
                node=node.right;
            }
        }
        return ans;
    }

中序遍历的迭代算法同前序遍历相比差别不大，也是采用两层while循环进行迭代，不同的是对于节点值得访问顺序，因为中序遍历是按照左-中-右顺序，因此访问节点值必然是在遍历完左节点之后再进行，因此代码实现是在第一层循环结束之后，取出栈中节点后，在获取右节点之前，访问节点值。

后序遍历

在上图中执行中序遍历算法得到的结果将会是

递归算法

public List<Integer> postorderTraversal(TreeNode root){
        List<Integer> ans = new LinkedList<>();
        postorderDfs(root, ans);
        return ans;
    }

    private void postorderDfs(TreeNode node, List<Integer> ans) {
        if (node==null)
            return;
        inorderDfs(node.left, ans);
        inorderDfs(node.right,ans);
        ans.add(node.val);
    }

迭代算法

后序遍历的迭代算法较上面两种而言更加复杂

public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) {
            return res;
        }

        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode prev = null;
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if (root.right == null || root.right == prev) {
                res.add(root.val);
                prev = root;
                root = null;
            } else {
                stack.push(root);
                root = root.right;
            }
        }
        return res;
    }

后序遍历同样是使用两次循环，遍历顺序是左-右-中，

在内循环中

while 节点不为空：

遍历左节点

左节点遍历完之后，有两种情况下访问当前节点值 root.val

if 当前节点无右子节点（无左右子节点即叶子结点）or 当前节点的右子节点是上一个访问节点值的节点（也就是说当前节点的左-右子节点都已经访问过了）：

自然是访问当前节点的值了

在每次访问节点值之后，记录一下节点。

else 也就是当前节点还有右子节点没有访问过：

当前节点进栈，访问右子节点

上述后序方法十分繁琐，理解起来也十分费劲，不过有一个更加容易理解的方法，联系前序遍历实现后序遍历

public List<Integer> postOrderTraversal(TreeNode root) {
        List<Integer> ans = new LinkedList<>();
        if (root == null)
            return ans;
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode node = root;
        while (!stack.isEmpty() || node!=null){
            if (node!=null){
                stack.push(node);
                ans.add(0, node.val);
                node = node.right;
            }else {
                node = stack.pop().left;
            }
        }
        return ans;
    }

后序遍历的顺序是 左-右-中，而前序遍历的顺序是中-左-右，现在对前序遍历做两步改动

将前序遍历中节点保存的时候，并不是放入集合的尾部，而是放入头部，那么结果顺序就变成了右-左-中
将前序遍历的顺序由从左到右改为从右到左，配合上一步，那么结果将会变为左-右-中，后序遍历就实现了

层序遍历

层序遍历没有递归实现方法，利用迭代实现对二叉树的广度优先搜索

public List<List<Integer>> levelOrderTraversal(TreeNode root){
        List<List<Integer>> ans = new LinkedList<>();
        if (root == null)
            return ans;
        Deque<TreeNode> stack = new ArrayDeque<>();
        int count =1;
        stack.addFirst(root);
        while (!stack.isEmpty()){
            int len = count;
            count=0;
            List<Integer> path = new LinkedList<>();
            for (int i = 0; i < len; i++) {
                TreeNode node = stack.pollLast();
                path.add(node.val);
                if (node.left!=null){
                    stack.addFirst(node.left);
                    count++;
                }
                if (node.right!=null){
                    stack.addFirst(node.right);
                    count++;
                }
            }
            ans.add(path);
        }
        return ans;
    }

利用变量count记录每层的结点数，利用栈存储节点，使用count的作用是在结果集合中，值可以分层存放。

到这里基本上就结束了，二叉树遍历重中之重的是二叉树的后序遍历迭代算法，分为一般思路方法以及将前序遍历一步步变成后序遍历的方法

This site is open source. Improve this page.