满嘴都是糖果
构造大顶堆

由于树结构存在next指针等数据,因此使用树结构构造大顶堆往往比较吃内存。由于堆结构为完全二叉树,仅使用数组即可构造大顶堆,父节点与左右子节点位置关系为: 父节点 arr[i],左子节点 arr[2* i],右子节点arr[2* i+1]
完全二叉树中 叶子节点数量=非叶子节点数量(+1),是否+1视这颗完全二叉树是否以左子树结束
在构造大顶堆时,以最底层最后一个非叶子节点开始构造(下图为了避免节点不是那么拥挤,将结尾的左子树移到了右子树)
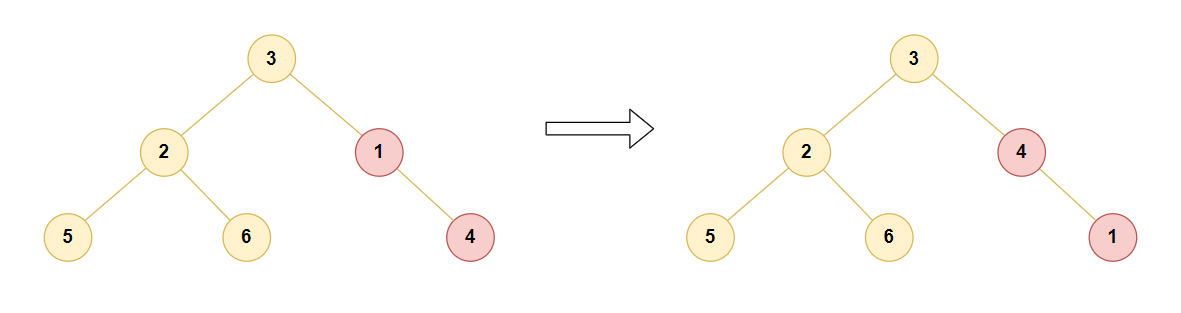
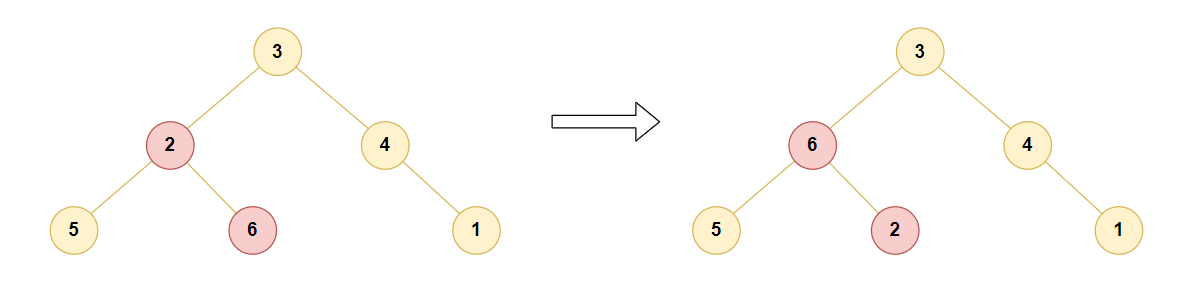
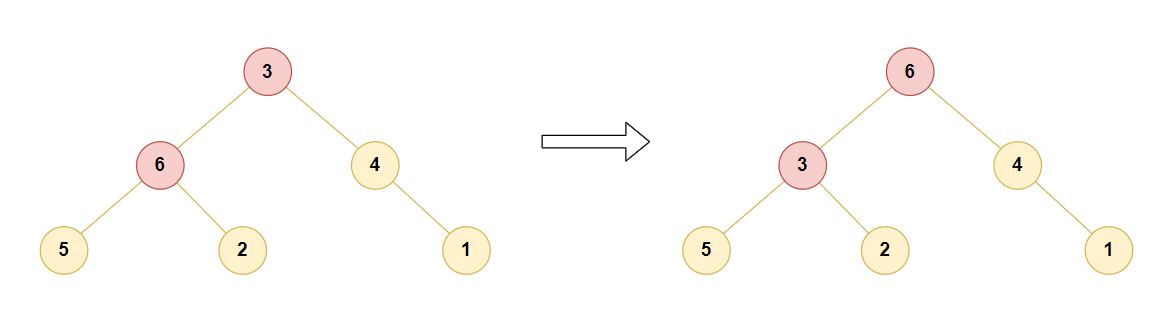
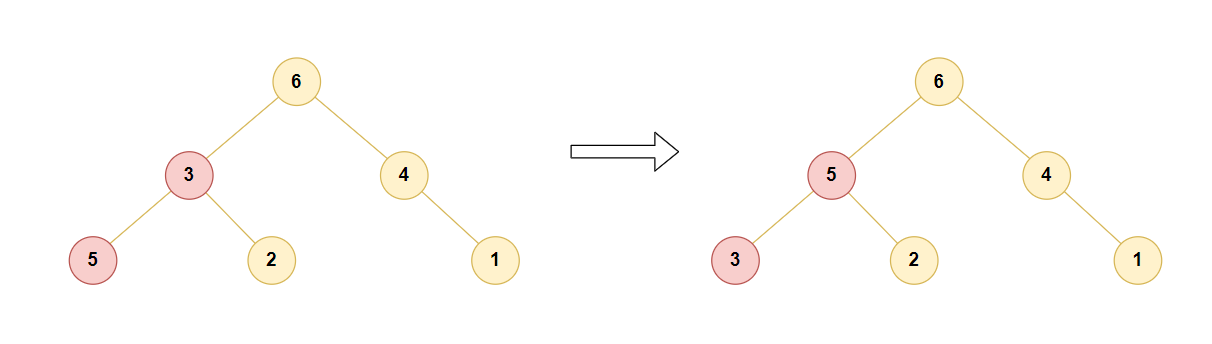
public int[] sortArray(int[] nums) {
buildHeap(nums,nums.length);
for (int len = nums.length-1;len>0;len--){
swap(nums,0,len);
updateHeap(nums,0,len);
}
return nums;
}
private void buildMaxHeap(int[] nums, int heapSize) {
//heapSize指将nums中前heapSize个数构造大顶堆
//逐层构建非叶子节点,非叶子节点数为heapSize/2
for (int i=heapSize/2;i>=0;i--){
//更新大顶堆中第i个编号的非叶子节点
updateMaxHeap(nums, i, heapSize);
}
}
private void updateMaxHeap(int[] nums, int i, int heapSize) {
//编号为i的节点的左节点以及右节点,large存放当前节点i与两个子节点中最大值所在的节点编号
int left = i*2+1,right=i*2+2,large=i;
//left要在范围内,并且大于父节点i
if (left<heapSize && nums[left]>nums[large]){
large=left;
}
//right要在范围内,并且大于父节点i
if (right<heapSize && nums[right]>nums[large]){
large=right;
}
//如果最大值节点不是父节点i,那么说明以i为根节点的树要进行调整
if (large!=i){
//交换父节点i与最大值节点large的值
swap(nums,i,large);
//由于large节点中值变为父节点值,这就不能保证以large节点为根节点的树满足大顶堆要求
//运用递归对large节点进行调节
updateMaxHeap(nums,large,heapSize);
}
}
private void swap(int[] nums, int i, int large) {
int tmp = nums[i];
nums[i] = nums[large];
nums[large] = tmp;
}