满嘴都是糖果
基本思想
快速排序的主要思想是通过划分将待排序的序列分成前后两部分,其中前一部分的数据都比后一部分的数据要小,然后再递归调用函数对两部分的序列分别进行快速排序,以此使整个序列达到有序。
步骤:
- 选定Pivot中心轴
- 将大于Pivot的数字放在Pivot的右边
- 将小于Pivot的数字放在Pivot的左边
- 分别对左右子序列重复前三步
那么问题来了,是如何将大于或者小于Pivot的数字进行移动的呢?
在本文中,始终将待排序数组的第一个数字选取为Pivot主元,通过数组的left和right两个指针的交替移动实现数字的归位
首先将Pivot值备份,left指针指向数组第一个位置,right指向最后一个位置,首先比较right指针
right指针操作
- 指针的值大于Pivot,该值无需换位,right-1,继续right指针操作
- 指针的值小于Pivot,将该值放入到left指针指向的位置,left+1,轮换到left指针操作
left指针操作
- 指针的值大于Pivot,将该值放入到right指针指向的位置,right-1,轮换到right指针做操作
- 指针的值小于Pivot,该值无需换位,left+1,继续left指针操作
直至left指针与right指针相遇,相遇的位置存放Pivot值
实例
以数组arr=[4, 2, 5, 6,3]为例,选取数组最左边值4作为Pivot=arr[0],right指针开始工作
1、arr[right]<Pivot,将3复制到arr[left],arr[left]=arr[right],left=left+1,轮到left指针工作

2、arr[left]<Pivot,不做处理,依旧是left指针工作,left=left+1
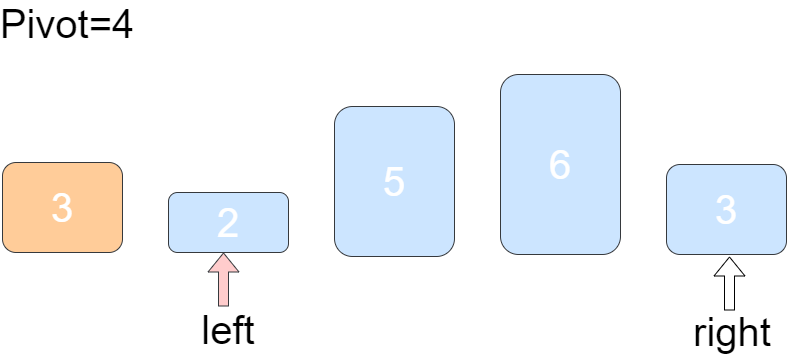
3、arr[left]>Pivot,将5复制到arr[right],arr[right]=arr[left],轮到right工作,right=right-1

4、arr[right]>Pivot,不做处理,依旧是left指针工作,left=left+1

5、arr[right]>Pivot,不做处理,依旧是right指针工作,right=right-1

6、此时left指针和right指针碰到一起,将此处的值赋为Pivot,arr[right]=Piovt

对于较为有序的数组,使用快速排序容易造成单次执行后主元两端的元素数目差异过大,因此我们在实现时,选取左右指针之间随机位置的数组值作为我们的主元,将该位置与left位置值作换位操作,基于随机选取主元的快速排序时间复杂度为期望 O(nlogn)。
import java.util.Random;
public class Solution {
public int[] sortArray(int[] nums) {
partition(nums,0,nums.length-1);
return nums;
}
private void partition(int[] nums, int left, int right){
if (left>=right)
return;
int l = left, r = right;
//随机选一个作为我们的主元
int i = new Random().nextInt(r - l + 1) + l;
int pivot = nums[i];
swap(nums, i, l);
//true->left指针工作,false->right指针工作
boolean flag = false;
while (left<right){
if(flag){
if (nums[left]>pivot){
nums[right] = nums[left];
right--;
flag = false;
}else {
left++;
}
}else {
if (nums[right]<pivot){
nums[left] = nums[right];
left++;
flag = true;
}else {
right--;
}
}
}
nums[right] = pivot;
partition(nums,l,left-1);
partition(nums,right+1,r);
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
}